Aplicação da acústica geométrica em medições

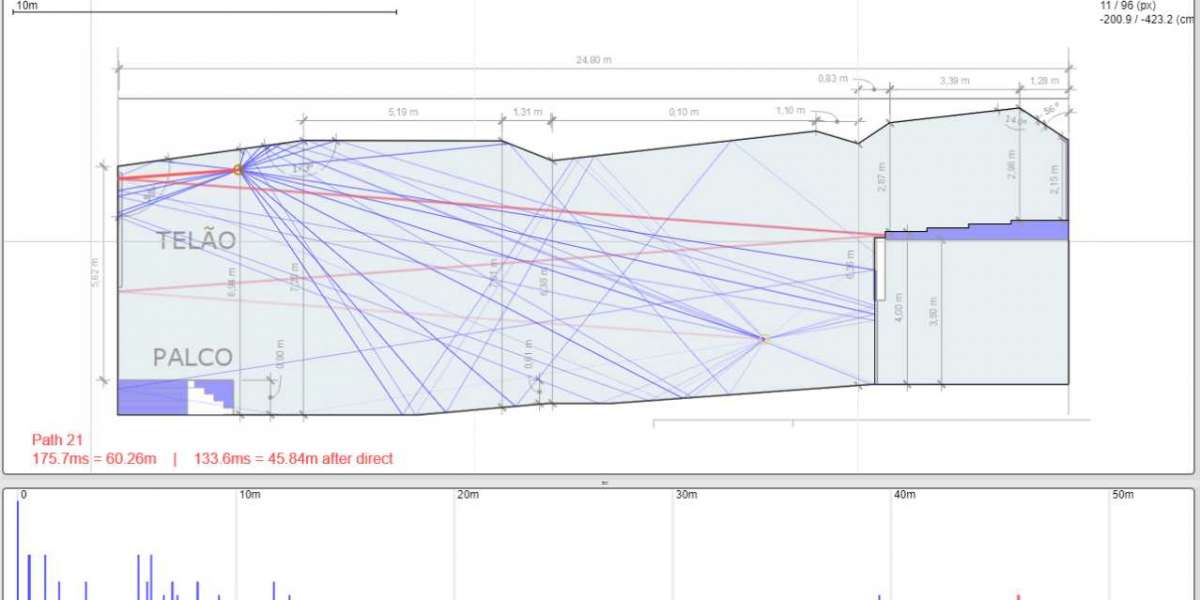
Antes de iniciarmos essa jornada, é preciso explicar que, antes de efetuar qualquer medição acústica, é de extrema importância considerarmos a acústica geométrica e suas contribuições no ambiente medido. Somatórios mal calculados devido a um posicionamento mal planejado, podem comprometer resultados e consequentemente, gerar falsos resultados em Laudos de ruído.

Ao entendermos o conceito "espacial" da propagação sonora, mesmo que de forma simplória, conseguimos melhor avaliar ambientes e situações e assim, aplicar o conceito em medições acústicas, seja pela NBR-10.151, ou para qualquer outra norma.

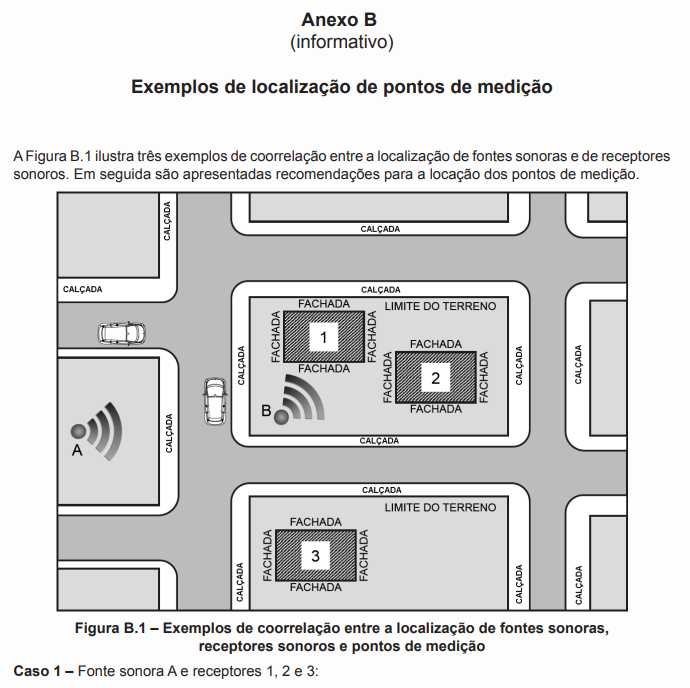
Quando na norma são pedidos 3 ou mais pontos de medição em ambientes internos, afastamentos mínimos de superfícies reflexivas ou janelas abertas, ou como posicionar os instrumentos em medições externas conforme demonstrado no mapa do Anexo B, da ABNT 10151, que indica qual conceito e lógica aplicar no posicionamento dos instrumentos de medição em ambientes externos, essas medidas são pensadas de modo a evitar somatórios ou influências indesejadas que possam interferir no resultado, tanto para mais, quanto para menos, devido à influência de superfícies reflexivas ou obstáculos que funcionem como barreiras absorvedoras no caminho da onda sonora que, por vezes, altera completamente o resultado das medições.

Acústica geométrica

A acústica geométrica, também conhecida como acústica de raios, é um ramo da acústica que estuda a propagação do som com base no conceito de Traço de Raios. Os raios são inicialmente representados como linhas retas, ao longo das quais a energia acústica é transportada. Este conceito é semelhante ao conceito da ótica geométrica, ou ótica de raios, que estuda a propagação da luz da mesma maneira.

A acústica geométrica é uma teoria aproximada, válida quando o comprimento das ondas acústicas forem muito pequenas, ou para frequências muito altas. A principal tarefa da acústica geométrica é determinar as trajetórias dos raios sonoros em uma ambiente. Os raios têm seu formato mais simples em um meio homogêneo, onde são linhas retas.

Quando os parâmetros acústicos do meio são funções de coordenadas espaciais, as trajetórias dos raios tornam-se curvilíneas, descrevendo a reflexão do som, refração, focalização possível, etc.

As equações da acústica geométrica têm essencialmente a mesma forma que as da ótica geométrica. As mesmas leis de reflexão e refração valem para os raios de som e para os raios de luz.

A acústica geométrica não considera os efeitos de onda tão importantes como a difração, no entanto, fornece uma ótima aproximação quando o comprimento de onda é muito pequeno em comparação às dimensões características das inclusões não homogêneas, através das quais o som se propaga.

Descrição matemática

A discussão abaixo é de Landau e Lifshitz.

Se a amplitude e a direção de propagação variam lentamente ao longo das distâncias do comprimento de onda, uma onda sonora arbitrária pode ser aproximada localmente como uma onda plana. Neste caso, o potencial de velocidade pode ser escrito da seguinte forma:

\phi =\mathrm {e} ^{\mathrm {i} \psi }

Para onda plana $\psi ={\boldsymbol {k}}\cdot {\boldsymbol {r}}-\omega t+\alpha$ , Onde ${\boldsymbol {k}}$ é um vetor de número de onda constante, $\omega$ é uma frequência constante, ${\boldsymbol {r}}$ é o vetor de raio, $t$ é a hora e $\alpha$ é alguma constante complexa arbitrária. A função $\psi$ é chamado de eikonal. Esperamos que o eikonal varie lentamente com coordenadas e tempo consistentes com a aproximação, então, nesse caso, uma expansão da série de Taylor fornece

\psi =\psi _{o}+{\boldsymbol {r}}\cdot {\frac {\partial \psi }{\partial {\boldsymbol {r}}}}+t{\frac {\partial \psi }{\partial t}}.

Igualando os dois termos para $\psi$ , encontra-se

{\boldsymbol {k}}={\frac {\partial \psi }{\partial {\boldsymbol {r}}}},\quad \omega =-{\frac {\partial \psi }{\partial t}}

Para ondas sonoras, a relação $\omega ^{2}=c^{2}k^{2}$ detém, onde $c$ é a velocidade do som e $k$ é a magnitude do vetor do número de onda. Portanto, o eikonal satisfaz uma equação diferencial parcial não linear de primeira ordem ,

\left({\frac {\partial \psi }{\partial x}}ight)^{2}+\left({\frac {\partial \psi }{\partial y}}ight)^{2}+\left({\frac {\partial \psi }{\partial z}}ight)^{2}-{\frac {1}{c^{2}}}\left({\frac {\partial \psi }{\partial t}}ight)^{2}=0.

Onde $c$ pode ser uma função de coordenadas se o fluido não for homogêneo.

A equação acima é igual à equação de Hamilton-Jacobi, onde o eikonal pode ser considerado como a ação. Uma vez que a equação de Hamilton-Jacobié equivalente às equações de Hamilton , por analogia, verifica-se que

{\frac {\mathrm {d} {\boldsymbol {k}}}{\mathrm {d} t}}=-{\frac {\partial \omega }{\partial {\boldsymbol {r}}}},\quad {\frac {\mathrm {d} {\boldsymbol {r}}}{\mathrm {d} t}}={\frac {\partial \omega }{\partial {\boldsymbol {k}}}}

Aplicações práticas

As aplicações práticas dos métodos da acústica geométrica podem ser encontradas em áreas muito diferentes da acústica. Por exemplo, na acústica arquitetônica, as trajetórias retilíneas dos raios sonoros permitem determinar o tempo de reverberação de uma forma muito simples. A operação de fatômetros e hidrolocadores é baseada em medições do tempo necessário para os raios sonoros viajarem até um objeto refletivo e vice-versa. O conceito de raio é usado na concepção de sistemas de focagem de som. Além disso, a teoria aproximada da propagação do som em meios não homogêneos (como, o oceano e a atmosfera) foi desenvolvida amplamente com base nas leis da acústica geométrica.

Os métodos de acústica geométrica têm um alcance limitado de aplicabilidade, porque o próprio conceito de raio só é válido para os casos em que a amplitude e a direção de uma onda sofrem pequenas mudanças em distâncias da ordem do comprimento de uma onda sonora. Mais especificamente, é necessário que as dimensões das salas ou obstáculos no caminho do som sejam muito maiores que o comprimento de onda. Se as dimensões características de um determinado problema se tornam comparáveis ao comprimento de onda, então a difração de onda começa a desempenhar um papel importante, e isso não é coberto pela acústica geométrica.

Aplicações de Software

O conceito de acústica geométrica é amplamente utilizado em softwares de simulação acústica. Alguns softwares que utilizam o traço de raios na acústica geométrica em seus cálculos, são o Enhanced Acoustic Simulator for Engineers e o Olive Tree Lab Terrain.

Atualmente a Acústica Fácil está desenvolvendo duas ferramentas baseadas nesse conceito, uma ferramenta chamada Calc-dB Propaga e a ferramenta chamada Calc-dB Trace. A primeira é voltada para análise de propagação sonora pela ISO 9613 com mapeamento colorizado em 2D e 3D, e a segunda, uma calculadora de traçado de raios simplificada em 2D, para análises preliminares para a concepção de sistemas de focagem de som, comportamento e propagação sonora em ambientes internos como salas de concerto, estúdios ou casas de shows, ou em ambientes externos, para análise de posicionamento de medidores de pressão sonora baseados em fotos aéreas 2D do Google, por exemplo.

Referências

"Acústica geométrica" . O Dicionário Gratuito . Recuperado em 29 de novembro de 2011 .
Landau, LD, Sykes, JB (1987). Mecânica dos fluidos: Vol 6.
Urick, Robert J. Princípios do som subaquático, ó edição. Nova york. McGraw-Hill, 1983.
CH Harrison, Ocean propagation models, Applied Acoustics 27, 163-201 (1989).

Acústica geométrica na ANBT NBR-10.151

Aplicação da acústica geométrica em medições

Acústica geométrica

Descrição matemática

Aplicações práticas

Aplicações de Software

Referências

CalcdB Tools

Acústica geométrica na ANBT NBR-10.151

Aplicação da acústica geométrica em medições

Acústica geométrica

Descrição matemática

Aplicações práticas

Aplicações de Software

Referências

CalcdB Tools

Symphony Hall, Boston

Estúdios e Home Studios Parte 2

Segurança baseada em comportamento